Setting up a molecule pair

Monomer

MonomerType enum is used to distinguish between systems of different types and stores the phase point size.
The size of phase point is calculated as size(phase_point) = MonomerType % MODULO_BASE, where MODULO_BASE is defined to 100 by default. The MonomerType enumeration contains the following values:

MonomerType::ATOM - Represents an atom with phase point size 0.
MonomerType::LINEAR_MOLECULE - Represents a linear molecule with phase point size 4.
MonomerType::LINEAR_MOLECULE_REQ_INTEGER - Represents a linear molecule with integer angular momentum with phase point size 4.
MonomerType::LINEAR_MOLECULE_REQ_HALFINTEGER - Represents a linear molecule with half-integer angular momentum with phase point size 4.
MonomerType::ROTOR - Represents a rotor with phase point size 6.
MonomerType::ROTOR_REQUANTIZED_ROTATION - Represents a rotor with requantized rotation with phase point size 6.

Monomer represents a monomer in a pair with associated dynamic variables. The order of variables in the qp array is specified by the following indices:

IPHI = 0
IPPHI = 1
ITHETA = 2
IPTHETA = 3
IPSI = 4
IPPSI = 5

The apply_requantization will be set to true in function computing the right-hand side values of Hamilton equations of motion (within rhs) to signal that the requantization of the monomer’s angular momentum is required at the current step of the trajectory propagation.

Notes:

17.01.2025: renamed I[3] to II[3] to avoid collision when including the header file complex.h

Monomer has the following fields:

Monomer::t – Type identifier for the monomer.
Monomer::II – Values of inertia tensor.
Monomer::DJ – Centrifugal distortion constant.
Monomer::qp – Dynamic variables (Euler angles and conjugated momenta).
Monomer::dVdq – Derivatives of potential energy with respect to coordinates pertaining to this monomer (the order of coordinates is the same as for qp).
Monomer::apply_requantization – Flag indicating whether requantization should be applied.
Monomer::req_switch_counter – Counter for tracking requantization switching events during the single trajectory.
Monomer::torque_cache_len – Length of the torque cache array.
Monomer::torque_limit – Torque limiting values to decide when requantization should be switched on/off.
Monomer::torque_cache – Cached torque values.

Molecule System

Angular variables and conjugated momenta are stored within the MoleculeSystem struct in the same order as within the qp of Monomer struct. The variables' indices in the intermolecular_qp array are defined as follows:

IPHI = 0
IPPHI = 1
ITHETA = 2
IPTHETA = 3
IR = 4
IPR = 5

Keep in mind that intermolecular coordinates and monomer's coordinates are not stored contiguously (monomer's coordinates are stored within the Monomer structure). The contiguous vector of coordinates can be assembled by calling extract_q_and_write_into_ms function, which stores the coordinates in memory pointed at by intermediate_q. These coordinates are passed to external functions that compute the values of intermolecular energy, its derivatives with respect to coordinates and induced dipole. There is no guarantee that coordinates stored in Monomer's and coordinates in memory at intermediate_q are always in sync. The function extract_q_and_write_into_ms must be invoked if the contiguous vector of coordinates is desired at a certain point of the program execution. MoleculeSystem has the following fields:

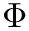
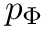
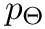
MoleculeSystem::intermolecular_qp – Coordinates and conjugated momenta that correspond to the intermolecular motion ( $\Phi$ , $p_\Phi$ , $\Theta$ , $p_\Theta$ , , ) .
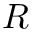
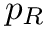
MoleculeSystem::m1 – First monomer.
MoleculeSystem::m2 – Second monomer.
MoleculeSystem::mu – Reduced mass of molecule pair.
MoleculeSystem::Q_SIZE – Total number of coordinates for molecule pair.
MoleculeSystem::QP_SIZE – Total number of coordinates and momenta for molecular pair (phase point size).
MoleculeSystem::intermediate_q – Contiguous vector of coordinates.
MoleculeSystem::dVdq – Contiguous vector of potential energy derivatives.
MoleculeSystem::init_rawtime – Initialization time represented as the number of seconds since Unix Epoch; set in init_ms.
MoleculeSystem::temp_rawtime – A temporary time field for the time at which the previous iteration of the iterative algorithm was completed; used for tracking elapsed time between iterations.

Function init_ms prepares the MoleculeSystem based on the specified monomer types, sets up memory buffers and initializes random number generator.

Parameters

mu	Reduced mass of the molecule pair
t1	Type of the first monomer
t2	Type of the second monomer
I1	Inertia tensor values for the first monomer. If the monomer is MonomerType::ATOM, no values will be read from the pointer, so NULL can be passed. Two and three values are expected for linear molecule (MonomerType::LINEAR_MOLECULE, MonomerType::LINEAR_MOLECULE_REQ_INTEGER and MonomerType::LINEAR_MOLECULE_REQ_HALFINTEGER) and rotor (MonomerType::ROTOR and MonomerType::ROTOR_REQUANTIZED_ROTATION).
I2	Inertia tensor values for the second monomer.
seed	Seed to set up random number generator (Mersenne Twister). A unique seed will be produced if 0 value is passed.

Function init_ms_from_monomers prepares the MoleculeSystem based on the provided Monomer structs, sets up memory buffers and initializes random number generator.

Pair State

PairState is an enumeration representing the possible states of a pair.

Calculations with prepared MoleculeSystem can conducted for the following pair states:

PairState::PAIR_STATE_FREE_AND_METASTABLE - Free and metastable states (TODO: automatically separate the contributions based on the number of turning points).
PairState::PAIR_STATE_BOUND - Bound states.
PairState::PAIR_STATE_ALL - Represents the totality of all possible states (aggregate value).

Energy calculations: core components

Function kinetic_energy computes the kinetic energy at the phase-point stored in MoleculeSystem.
The kinetic energy in the laboratory frame of reference is calculated in parts. The part corresponding to intermolecular degrees of freedom:

$T_\textrm{int} = \frac{p_R^2}{2 \mu} + \frac{p_\Theta^2}{2 \mu R^2} + \frac{p_\Phi^2}{2\mu R^2 \sin^2 \Theta};$

to linear molecule:

$T_\textrm{lin} = \frac{p_\theta^2}{2 I} + \frac{p_\varphi^2}{2 I \sin^2 \theta};$

and to rotor:

$T_\textrm{rotor} = \frac{1}{2 I_1 \sin^2 \theta_2} \Big[ \left( p_\varphi - p_\psi \cos \theta \right) \sin \psi + p_\theta \sin \theta \cos \psi \Big]^2 \\ + \frac{1}{2 I_2 \sin^2 \theta} \Big[ \left( p_\varphi - p_\psi \cos \theta \right) \cos \psi - p_\theta \sin \theta \sin \psi \Big]^2 \\ + \frac{1}{2 I_3} \left( p_\psi \right)^2.$

Function Hamiltonian calls kinetic_energy function to compute kinetic energy, assembles a contiguous vector of coordinates via calling extract_q_and_write_into_ms and passes it to external pes function. The obtained values are added and returned.

pes function accepts an array of Q_SIZE variables. MoleculeSystem describes the order of variables. The pointer to pes is a global variable in hawaii.c file. The potential energy function is loaded from the dynamic library (see keyword SO_POTENTIAL in Input File Description). Intermolecular distance is measured in Bohrs, while angles are measured in radians. The function is expected to return energy in units of Hartree.

dpes function accepts an array of Q_SIZE variables. MoleculeSystem describes the order of variables. The pointer to dpes is a global variable in hawaii.c file. The derivative of potential energy function is loaded from the dynamic library (see keyword SO_POTENTIAL in Input File Description). Intermolecular distance measured in Bohrs, while angles are measured in radians. The function is expected to return an array of derivatives of energy in units of Hartree/Bohr of length Q_SIZE.

dipolePtr

Sampling the phase-space point

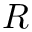
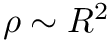
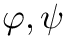
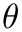
Function q_generator generates with density $\rho \sim R^2$ in the range [params.sampler_Rmin, params.sampler_Rmax]. The distributions of $\varphi, \psi$ are $\varphi, \psi \sim U[0, 2\pi]$ and for $\theta$ is $\cos \theta \sim U[0, 1]$ . Implemented for intermolecular degrees of freedom, linear molecule and rotor.

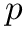
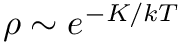
Function p_generator samples momenta from distribution $\rho \sim e^{-K/kT}$ at given temperature.

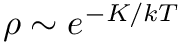
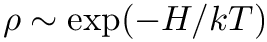
reject applies the rejection step to the phase-point that is stored in the MoleculeSystem. It presupposes that the provided phase-point is sampled from $\rho \sim e^{-K/kT}$ using q_generator and p_generator functions. The random variable $u \sim U[0, 1]$ is chosen, to determine whether the current phase-point is to be accepted with probability $\rho \sim \exp(-H/kT)$ .

Propagating trajectories

Trajectory has the following fields:

Trajectory::ms – Pointer to MoleculeSystem.
Trajectory::DIM – Number of Hamilton's equations of motion (system dimension).
Trajectory::mxsteps – Maximum number of internal time steps for the solver.
Trajectory::y – Internal phase-space vector (current step of the system).
Trajectory::abstol – Absolute tolerance for each variable in the ODE system.
Trajectory::reltol – Relative tolerance for the ODE solver.
Trajectory::A – Matrix structure for storing jacobian information.
Trajectory::LS – Linear solver object for the ODE system.
Trajectory::cvode_mem – Pointer to the CVODE memory block (solver internal state).
Trajectory::temp_qp – Temporary storage array for coordinates and momenta during trajectorypropagation.
Trajectory::ic – Initial conditions for the trajectory.
Trajectory::check_energy_conservation – Flag indicating whether to monitor energy conservation during trajectory propagation.
Trajectory::E0 – Initial total energy of the system (used for conservation checks).
Trajectory::E_last – Energy value from the last computed step (for tracking changes in energy).

init_trajectory initializes a Trajectory structure for propagating Hamilton's equations of motion for the provided molecule system. The trajectory will be configured with the specified with the specified relative tolerance for numerical integration. The returned Trajectory should be properly freed using free_trajectory after use to avoid memory leaks.

rhs function is passed to CVode library to propagate the trajectory. First, the phase-point coordinates are stored into MoleculeSystem struct. A contiguous vector of coordinates is assembled via extract_q_and_write_into_ms. Next, by calling the external function dpes, the derivatives of potential energy are computed and stored into MoleculeSystem::dVdq field. The components of derivative vector are then copied into the field Monomer::dVdq of the corresponding Monomer via the call to extract_dVdq_and_write_into_monomers. The right-hand side of Hamilton's equations with respect to intermolecular degrees of freedom are readily obtained and filled into output ydot, while the derivatives with respect to monomer's coordinates are handled by rhsMonomer function.

rhsMonomer dispatches between computing the right-hand side of Hamilton's equations of motion depending on the type of monomer. In addition to differentiating the kinetic energy, the derivatives of potential energy, which are taken from Monomer::dVdq, are also added to compute the right-hand side.
rhsMonomer does not account for requantization which should happen after this function has been called.

compute_numerical_rhs Computes the right-hand side of Hamilton's equations of motion using finite-difference formulas. The returned Array contains derivatives whose order corresponds to variable ordering employed in the MoleculeSystem structure.

Parameters

ms	Pointer to the MoleculeSystem for which to compute the derivatives.
order	Order of the finite-difference formula to employ for calculation.

compute_numerical_derivatives

compute_numerical_jac

free_trajectory

make_step Invokes the main function of CVode and, if enabled, applies requantization to the monomers' angular momenta. When the apply_requantization flag within the MoleculeSystem is set, * the momenta in qp are rescaled to adjust the angular momentum to the nearest half-integer or integer, according to the requantization rule which is represented within the Monomer type. Subsequently, the function synchronizes the internal trajectory phase-space vector with the MoleculeSystem's phase-space vector, and reinitializes the state of CVode to reset its state since a sudden change of phase-point has occured.

set_initial_condition

make_vector

set_tolerance

Conducting angular momentum requantiation

j_monomer computes the magnitude of angular momentum of passed-in monomer. Currently, implemented only for linear molecules.

$[\textrm{linear molecule}]: j = \begin{bmatrix} - p_\theta \sin \varphi - p_\varphi \cos \varphi / \tan \theta \\ p_\theta \cos \varphi - p_\varphi \sin \varphi / \tan \theta \\ p_\varphi \end{bmatrix}$

torque_monomer computes the magnitude of torque (time-derivative of angular momentum) of passed-in monomer. Requires the derivative of potential Monomer::dVdq to be set within the monomer. Currently, implemented only for linear molecules.

$[\textrm{linear molecule}]: \tau = \begin{bmatrix} \displaystyle \sin \varphi \frac{\diff{V}}{\diff{\theta}} + \cos \varphi / \tan \theta \frac{\diff{V}}{\diff{\varphi}} \\ \displaystyle -\cos \varphi \frac{\diff{V}}{\diff{\theta}} + \sin \varphi / \tan \theta \frac{\diff{V}}{\diff{\varphi}} \\ \displaystyle -\frac{\diff{V}}{\diff{\varphi}} \end{bmatrix}$

find_closest_integer requantization to: 0.0, 1.0, 2.0, 3.0 ...

find_closest_half_integer requantization to: 0.0, 0.5, 1.5, 2.5, 3.5 ...

Computing averages over the phase space

calculate_M0 Running mean/variance formulas taken from GSL 1.15 https://github.com/ampl/gsl/blob/master/monte/plain.c

mpi_calculate_M0

calculate_M2 Running mean/variance formulas taken from GSL 1.15 https://github.com/ampl/gsl/blob/master/monte/plain.c

mpi_calculate_M2

compute_dHdp

transform_variables Input: n-dimensional point in [0; 1]^n hypercube Output: [std::vector<double>] point in phase space [double] cumulative jacobian of the transform

integrand_pf

integrand_M0

integrand_M2

mpi_perform_integration

Performing averaging over trajectory ensembles

calculate_correlation_and_save TODO: check 'sampler_Rmin': we want to catch the situation when it's too low for given Temperature

calculate_correlation_array_and_save

calculate_spectral_function_using_prmu_representation_and_save

correlation_eval

correlation_eval_zimmerman_trick

invert_momenta

Processing the results

Smoothing

Here is the link to description of LOESS module