Navigation

Introduction

Problems addressed by library

Compute statistical averages over ensembles of classical trajectories restricted by chosen phase-space domains (e.g., bound or unbound states), enabling the calculation of dipole autocorrelation functions.
Calculate static phase-space averages using rejection sampling and adaptive Monte Carlo algorithms to estimate zeroth and second spectral moments.
Transform correlation functions into spectral functions, apply smoothing, and convert them into spectral profiles.

First, we outline the key objects and their corresponding units of measurement. In the context of this document, the correlation function of the dipole moment, 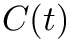, is defined as:

$C(t) = V \langle \mu(0) \mu(t) \rangle.$

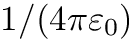
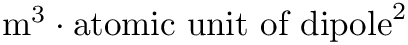
Note that this definition differs from others, such as the one in Ref. Chistikov2021, as it does not include the $1/(4 \pi \varepsilon_0)$ factor. Instead, this factor is incorporated into the definition of the spectral function. The correlation function values are produced by calculate_correlation_and_save and calculate_correlation_array_and_save in units of ( $\textrm{m}^3 \cdot \textrm{atomic unit of dipole}^2$ ). The time is treated internally in atomic time units, and the produced CFnc object stores the time in the atomic time units. The spectral function represented as SFnc object is defined as follows:

$G(\nu) = \frac{1}{2\pi} \frac{1}{4\pi \varepsilon_0} \int\limits_{-\infty}^{+\infty} C(t) e^{-2 \pi i c \nu t} \textrm{d}t,$

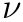
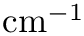
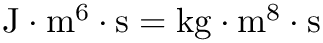
where $\nu$ is the wavenumber ( $\textrm{cm}^{-1}$ ). The values of spectral function are $\textrm{J} \cdot \textrm{m}^6 \cdot \textrm{s} = \textrm{kg} \cdot \textrm{m}^8 \cdot \textrm{s}$ .

The binary absorption coefficient stored as Spectrum is then related to the spectral function according to:

$\alpha(\nu) = \frac{\tau(\nu)}{\rho_1 \rho_2} = \frac{(2\pi)^4 N_L^2}{3 h} \nu \left[ 1 - \exp \left( -\frac{h c \nu}{k_\textrm{B} T} \right) \right] G(\nu),$

where the absorption coefficient is

$\tau(\nu) = L^{-1} \ln (I_0 / I),$

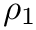
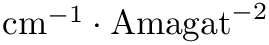
and $\rho_1$ and $\rho_2$ are gas densities in mixture. We will express the binary absorption coefficient as per convention in $\textrm{cm}^{-1}\cdot\textrm{Amagat}^{-2}$ .

Table of Contents

Navigation

Introduction

Main Functionality

Calculating correlation functions

Calculating spectral functions